毎日配信の頭をやわらか~くしてくれる脳トレクイズ。
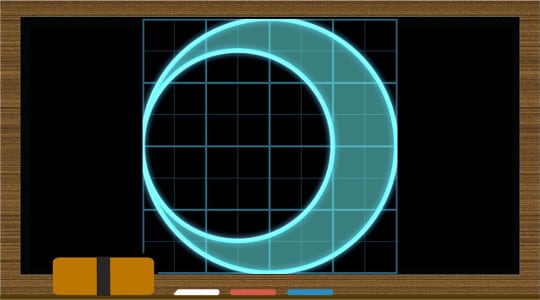
図形問題に挑戦しましょう! 小さい正方形の1辺を1、円周率をΠ(パイ)とすると、ハイライト部分の面積はいくつになるでしょうか? 半径の異なる円の面積を求めその差を計算すればいいのですが、先に半径の差を引きますか? どうやって答えを導けばいいでしょう?
![]()
こたえをみる
こたえをみる
【答】 7Π
大きい円の面積は4×4×Π=16Π、小さい円の面積は3×3×Π=9Πです。つまり、16Π-9Π=7Πがハイライトされた部分の面積ということになります。
ちなみに円周率を「3」にすると、大きい円の面積は4×4×3=48、小さい円の面積は3×3×3=27。差は48-27=21になり、これを円周率の3で割ると7となり(7Π)、上の計算が正しいとわかりますね。
大きい円の面積は4×4×Π=16Π、小さい円の面積は3×3×Π=9Πです。つまり、16Π-9Π=7Πがハイライトされた部分の面積ということになります。
ちなみに円周率を「3」にすると、大きい円の面積は4×4×3=48、小さい円の面積は3×3×3=27。差は48-27=21になり、これを円周率の3で割ると7となり(7Π)、上の計算が正しいとわかりますね。



