合否を分ける「算数」を得意にするには

こんにちは。中学受験専門塾 伸学会代表の菊池です。
中学受験でも高校受験でも大学受験でも、算数・数学は最も差がつきやすい科目です。
ですから、受験の合否は算数・数学が勝負を分けます。
そのため、私が指導している中学受験でも、ほとんどの子が、勉強時間に占める割合は算数が最も多くなります。
しかし、残念ながら、その努力がそのまま成果につながるとは限りません。
頑張って勉強しているのになかなか成績が上がらずつらい思いをする子も多いです。
あなたの周りにも、算数・数学が苦手で苦労している人がいませんでしたか?
果たして、すぐに算数の成績が上がる子と、なかなか成績が上がらない子の違いは何なのでしょうか?
今回はその違いについて、科学的な研究の結果も交えながらお話ししようと思います。
算数ができるようになるために必要な両輪
算数ができるようになるためには、土台となる能力と、公式や図の書き方といった解法の知識と、両者がバランスよく必要です。
わかりやすくイメージするために、サッカーで例えます。
速く走る・長時間走る・ボールを上手に蹴るといったものは、土台となる「能力」です。
これらは「速く走るためのフォーム」や「疲れにくい走り方のフォーム」、「上手にボールを蹴るためのフォーム」を言葉で説明してアドバイスすることはできます。
しかし、説明だけで身に着けさせることはできませんよね?
「能力」を鍛えるためには自分で練習する以外に方法はありません。
それに対して、この状況ではどのフォーメーションを採用するか、誰をマークし、誰にパスを出すべきかといった戦術は「知識」です。
「知識」は、言葉で説明して、教えることができます。
土台となる能力と戦術的な知識と、サッカー選手として活躍するためには両者が必要になるのはお分かりいただけるでしょうか?
算数の勉強においても同じようなことが言えます。
「数の大きさや割合の感覚」「図形の形をとらえる感覚」「空間・立体の感覚」などは土台となる「能力」です。
これらはボールの蹴り方や自転車の乗り方や泳ぎ方と同じく、言語化することが困難です。
ですから授業を聞いたところで理解することはできません。
鍛えるための基礎トレーニングを何度もやって、頭と体で覚えるしかないのです。
それに対して、この問題はどんな図や式を書けば良いかといった戦術は、「知識」として教えられます。
ですから、学校や塾での授業は、主にこの「知識」を学ぶ場になっています。
算数の成績を上げるためには「能力」と「知識」の両方を揃える必要があります。
そのことを示す研究として、例えばカーネギーメロン大学のリサ・ファツィオらが行ったこんなものがあります。
▼イメージを使う問題
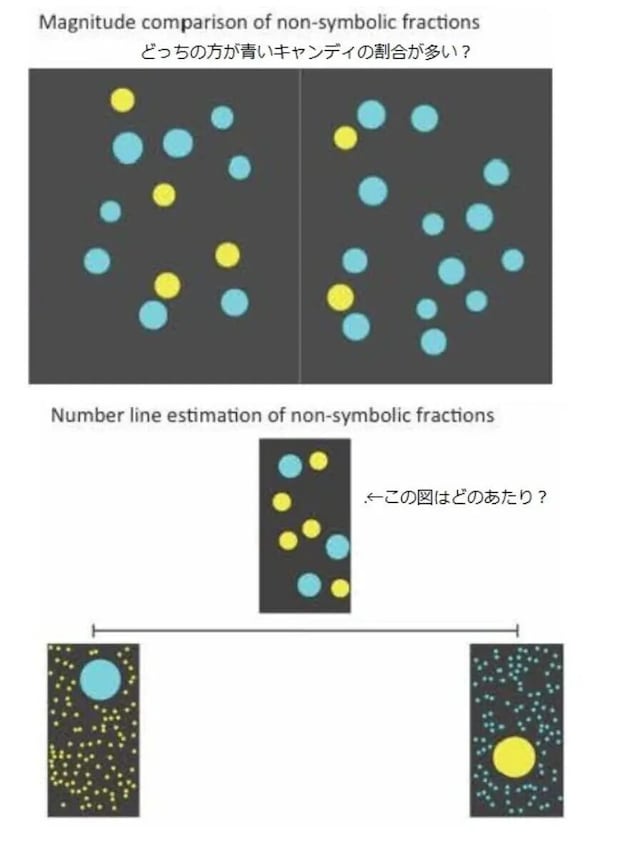
▼数式を使う問題

数式を使う問題
※図は参考文献[*1]より引用の上で日本語の注釈を追加
小学5年生の子供たちに、 イメージを使うタイプの問題(上段のようなもの)と、数式を使うタイプの問題(下段のようなもの)をたくさん解かせました。
また、これとは別に、算数の一般的なテストを受験させました。
そして、これらの点数を比較したところ、イメージを使う問題がよくできた子は、算数のテストの点数が高いことがわかりました。
また、数式を使った問題がよくできた子も、算数のテストの点数も高いことがわかりました。
しかし、イメージを使った問題の点数と、数式を使った問題の点数の間には関係がありませんでした。[*1]
算数ができるようになるためには、数をイメージでとらえる「能力」と、数式に関しての「知識」の両方が必要だということがわかります。
そして、これらは一方を鍛えればもう一方が自然と育つわけではないこともわかります。
何しろ「能力」と「知識」の成績の間には関係が無かったのですから。
だから、一方が足りない場合はそれを鍛えるためのトレーニングが必要ということなのです。
数をイメージでとらえる感覚だけでなく、図形の形をとらえる感覚、空間・立体の感覚も、それぞれ同様に、算数の「能力」に分類されます。
図形の面積や体積の公式という「知識」を知っていても、複雑な複合図形の中で「おうぎ形」や「台形」や「三角すい」が見えてくる「能力」がなければ、レベルの高い問題は解けないのです。

